Physics Joints

This guide discusses how to configure the various physical Box2D joints available in Corona.

Overview

Joints can be used to assemble complex physical objects from multiple rigid bodies. For example, joints can be used to join the limbs of a ragdoll figure, attach the wheels of a vehicle to its body, create a moving elevator platform, and more.

Creation and Removal

Most joints are used to connect two rigid physical bodies, so you must create these bodies first and then submit them as arguments to the physics.newJoint() constructor function, along with other properties that vary depending on the joint type (see details below).

physics.newJoint( jointType, ... )

If a joint is no longer needed, you can destroy it by calling either object:removeSelf() or display.remove():

joint:removeSelf()
display.remove( joint )

If one of the joined bodies is destroyed, the associated joint will be automatically destroyed. However, remember to properly remove and nil any references to a joint which has been destroyed.

Shared Properties/Methods

The following properties and methods apply to all joint types:

local ax, ay = myJoint:getAnchorA()
local bx, by = myJoint:getAnchorB()
local ax, ay = myJoint:getLocalAnchorA()
local bx, by = myJoint:getLocalAnchorB()
local reactionForceX, reactionForceY = myJoint:getReactionForce()

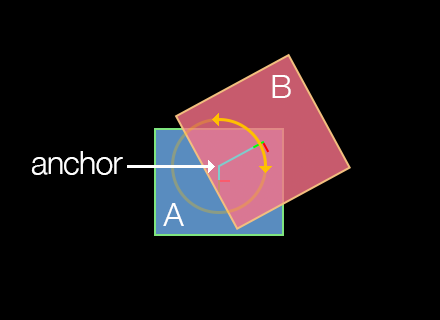
Pivot Joint

A pivot joint, known as a revolute joint in Box2D terms, joins two bodies at an overlapping point, like two boards joined by a rotating peg. The initial arguments are bodies A and B to join, followed by the x and y coordinates for the anchor point, declared in content space coordinates.

local pivotJoint = physics.newJoint( "pivot", bodyA, bodyB, anchor_x, anchor_y )

If you're building a complex assembly like a ragdoll with pivot joints and you're experiencing instability issues, consider setting physics.setContinuous() to true.

Joint Motor

Optionally, object B joined with a pivot joint to object A can be driven (rotated) with a joint motor. This rotation can be either clockwise or counter-clockwise, depending on the motorSpeed value. Note that joint motors have a fairly weak maximum torque by default, so setting motorSpeed may appear to have little visible effect. Therefore, you should generally set maxMotorTorque to a high value such as 100000 if you're trying to move any significant mass, such as rotating a wheel to power a car.

Rotation Limits

Pivot joints can optionally be constrained in their range of rotation. For example, if constructing a ragdoll figure, the head/neck joint would likely have a limited range of angular motion in either the clockwise or counter-clockwise direction.

  • pivotJoint.isLimitEnabled — Set this to true to constrain the pivot joint rotation limits.

  • pivotJoint:setRotationLimits() — Function which accepts two values, in degrees, defining the negative and positive limits of rotation. For example, if you want to limit the rotation somewhat tightly in relation to the upward axis (0), these values may be -10 and 10 respectively. Note that these values remain in relation to the rotation of body A, meaning that if body A rotates after the joint is declared, these rotation limits will remain in rotational synchronization with that body.

pivotJoint.isLimitEnabled = true
pivotJoint:setRotationLimits( -20, 20 )
local negLimit, posLimit = pivotJoint:getRotationLimits()
print( negLimit, posLimit )

Other

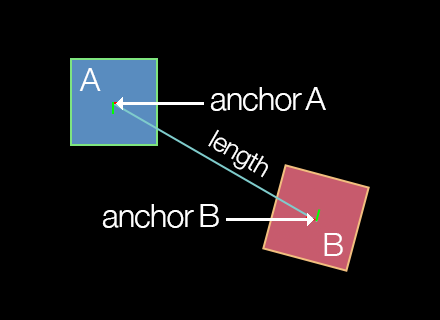
Distance Joint

A distance joint attaches two bodies at a fixed distance. The initial arguments are bodies A and B to join, followed by an x and y anchor point coordinate for each body, declared in content space coordinates.

local distanceJoint = physics.newJoint( "distance", bodyA, bodyB, anchorA_x, anchorA_y, anchorB_x, anchorB_y )

Damping/Frequency

Optionally, the distance joint can be made soft, like a spring-damper connection. Many factors can influence the behavior of a soft distance joint, including the mass of the attached bodies and forces upon them, so you should carefully test the specified values to achieve the desired simulation.

  • distanceJoint.dampingRatio — This number value can range from 0 (no damping) to 1 (critical damping). With critical damping, all oscillations should vanish.

  • distanceJoint.frequency — This number specifies the mass-spring damping frequency in Hz. A low value will make the joint extremely soft and cause it to contract with very low force.

  • distanceJoint.length — This number specifies the distance between the anchor points, which should not be zero or very short. If you position the bodies before applying a distance joint to them, this length will automatically be set as the distance between the anchor points, so it's usually not necessary to set this parameter.

Piston Joint

A piston joint, known as a prismatic joint in Box2D terms, joins two bodies along a single, restricted axis of motion, like engine pistons or an elevator platform that is restricted to movement along a vertical axis. The initial arguments are bodies A and B to join, followed by an x and y coordinate for an anchor point on either body, followed by values which define the axis along which linear motion is allowed.

local pistonJoint = physics.newJoint( "piston", bodyA, bodyB, anchor_x, anchor_y, axisX, axisY )

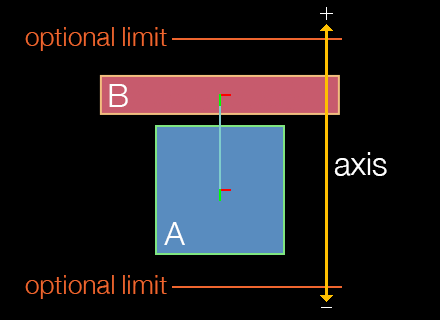
Motion Axis

As stated, piston joints have a restricted axis of linear motion, defined by axisX and axisY. This axis can be considered a directional vector indicating which way the object will move when driven by a positive pistonJoint.motorSpeed value.

The following chart provides examples of the relationship between axisX, axisY, and a positive motor speed. However, both axisX and axisY values can be decimal values ranging between -1.0 and 1.0 — you are not restricted to these eight directions.

axisX axisY Direction / Angle
0 -1 up / 0°
1 -1 right-up / 45°
1 0 right / 90°
1 1 right-down / 135°
0 1 down / 180°
-1 1 left-down / 225°
-1 0 left / 270°
-1 -1 left-up / 315°
Notes

  • To limit motion distance along the linear axis in either direction, use the pistonJoint:setLimits() function as illustrated below.

  • The speed of motion is not controlled by the axis values, but rather by the pistonJoint.motorSpeed property as explained in the next section.

  • A negative motor speed will drive the object in the opposite direction of its defined axis vector.

Joint Motor

Optionally, the piston joint can be driven with a joint motor. Unlike the rotational motor of the pivot joint, this motion will be linear, restricted along the defined axis. For example, a piston joint motor can be used to move an elevator platform up and down along its axis.

Motion Limits

Piston joints can optionally be constrained in their range of linear motion. The limits take the form of a lower and upper limit which define the range of motion (distance) along the axis defined by axisX and axisY.

  • pistonJoint.isLimitEnabled — Set this to true to limit the piston joint motion range.

  • pistonJoint:setLimits() — This function accepts two values which define the negative and positive range of motion. The second value should always be greater than or equal to the first value, since they define a range of motion (distance) along the axis.

pistonJoint.isLimitEnabled = true
pistonJoint:setLimits( -40, 120 )
local negLimit, posLimit = pistonJoint:getLimits()
print( negLimit, posLimit )

Other

Friction Joint

The friction joint is used to simulate top-down friction between two objects. This can be useful for simulating both translational (directional) friction and angular (rotational) friction between two joined objects. The initial arguments are bodies A and B to join, followed by an x and y coordinate for the anchor point.

local frictionJoint = physics.newJoint( "friction", bodyA, bodyB, anchor_x, anchor_y )

Friction Values

When creating a friction joint, simulated friction can be applied via maximum force and torque values:

  • frictionJoint.maxForce — This number specifies the maximum directional friction which may be applied to the joined body. A higher value simulates higher friction.

  • frictionJoint.maxTorque — This number specifies the maximum rotational friction which may be applied to the joined body. A higher value simulates higher friction.

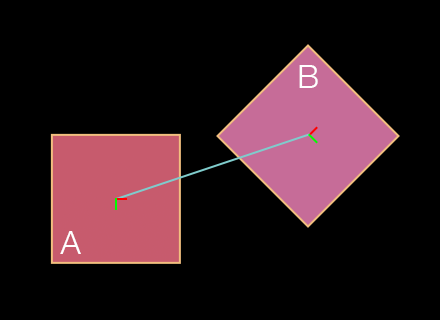
Weld Joint

The weld joint rigidly attaches two bodies at a specified anchor point in content space coordinates.

local weldJoint = physics.newJoint( "weld", bodyA, bodyB, anchor_x, anchor_y )

Damping/Frequency

Due to mathematical approximation, this joint may appear slightly soft during simulation, even if dampingRatio and frequency are set to prevent this behavior. If you want to assemble multiple shapes without any risk of flexing, consider creating a multi-element body as illustrated in the Physics Bodies guide.

  • weldJoint.dampingRatio — This number value can range from 0 (no damping) to 1 (critical damping). With critical damping, all oscillations should vanish.

  • weldJoint.frequency — This number value specifies the mass-spring damping frequency in Hz. A low value will make the joint extremely soft and allow for rotation around the anchor point.

Positioning

Notice in the diagram that the two bodies don't necessarily need to overlap, and the joint anchor doesn't necessarily need to reside within one of the bodies. In fact, the two bodies can be completely separated and the weld joint will still join the bodies together as if a rigid, invisible link exists between them.

Other

Wheel Joint

A wheel joint, known as a line joint in Box2D terms, is similar to a piston joint, except that the attached body can rotate freely like a wheel mounted to the shock absorber of a car. Most of its properties are inherited from the standard piston joint, but you can specify a mass-spring frequency and damping ratio. The initial arguments are bodies A and B to join, followed by an x and y coordinate for an anchor point on either body, followed by values which define the axis along which linear motion is allowed.

local wheelJoint = physics.newJoint( "wheel", bodyA, bodyB, anchor_x, anchor_y, axisX, axisY )

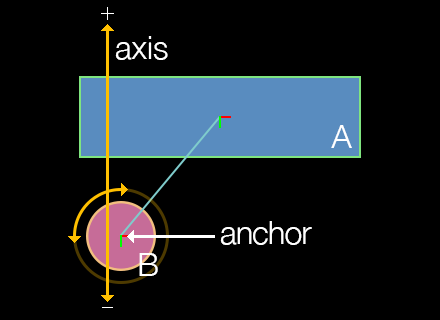
Motion Axis

Like the piston joint, wheel joints have a restricted axis of linear motion, defined by axisX and axisY. However, unlike piston joints, wheel joints aren't driven by a motor, so you can't send the wheel (body B in the diagram) moving in a specific direction based on the defined axis values. For example, setting these values to either 0,1 or 0,-1 will restrict motion to a vertical axis, but not restrict it to either upward or downward along that axis. Similarly, values of either 1,0 or -1,0 will restrict linear motion to either left or right along a horizontal axis.

Essentially, the wheel — or rather the object that represents the wheel — is prone to whatever forces might be upon it, for instance gravity. The object will attempt to stay upon the defined axis, but other forces may pull/push the wheel off of that axis in unpredictable ways.

Damping/Frequency

Optionally, the wheel joint can be made soft, like a spring-damper connection. Many factors can influence the behavior of a soft wheel joint, including the mass of the attached bodies and forces upon them, so you should carefully test the specified values to achieve the desired simulation.

  • wheelJoint.springDampingRatio — This number value can range from 0 (no damping) to 1 (critical damping). With critical damping, all oscillations should vanish.

  • wheelJoint.springFrequency — This number value specifies the mass-spring damping frequency in Hz. A low value will decrease simulated suspension. This value must be greater than 0.

Other

Pulley Joint

A pulley joint attaches two bodies with an imaginary rope whose length remains constant. If one body is pulled or pushed by some force, the other body will compensate according to the simulated rope. The initial arguments are bodies A and B to join, followed by two coordinate pairs which represent the stationary anchor points from where each side of the rope hangs. The next four arguments are the x and y anchor point coordinates (one for each body), followed by the final ratio value which can be adjusted to simulate a block and tackle setup.

local pulleyJoint = physics.newJoint( "pulley", bodyA, bodyB, statA_x, statA_y, statB_x, statB_y, bodyA_x, bodyA_y, bodyB_x, bodyB_y, 1.0 )

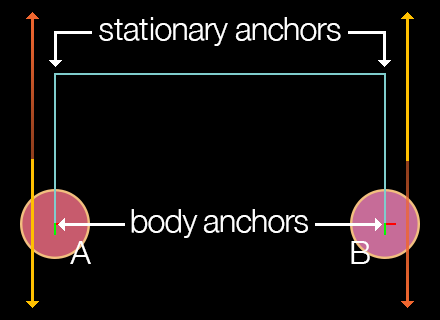
Pulley Ratio

The pulley joint features a ratio property as the final parameter in the constructor. This ratio can be adjusted to simulate a block and tackle arrangement. In such a scenario, one side of the pulley rope moves faster than the other. The default ratio is 1.0 which simulates a simple pulley.

Other

  • pulleyJoint:getGroundAnchorA() — This function returns the x and y coordinates of the joint's first ground anchor in content coordinates.

  • pulleyJoint:getGroundAnchorB() — This function returns the x and y coordinates of the joint's second ground anchor in content coordinates.

  • pulleyJoint.length1 — Read-only number value that, upon instantiation, indicates the distance in pixels between the first joint anchor point and its stationary pulley anchor point.

  • pulleyJoint.length2 — Read-only number value that, upon instantiation, indicates the distance in pixels between the second joint anchor point and its stationary pulley anchor point.

Touch Joint

A touch joint, known as a mouse joint in Box2D, connects a single object to an on-screen target point. This can be used to move an object to a target point by a theoretical elastic joint with variable strength and elasticity. The initial arguments are the body A to connect followed by the x and y anchor point coordinates in content space.

local touchJoint = physics.newJoint( "touch", body, anchor_x, anchor_y )

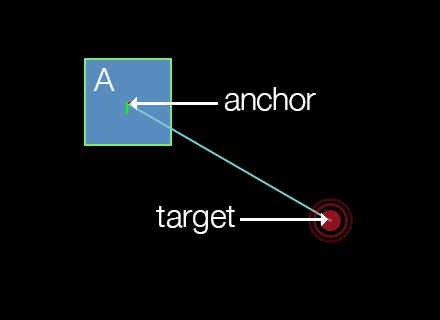
Anchor Point

For touch joints, the anchor point can be considered the point at which to "connect" the body. For example, to connect a body by its center point, specify body.x and body.y as the last two arguments. Alternatively, to drag an object by the point it was touched on, use the event.x and event.y values returned by the touch event. This anchor point is commonly configured as a point within the bounds of the body, although it can reside outside the bounds if desired.

Note that the body connected by the touch joint remains under simulation, so it will interact fully with the other bodies in the world. Also, the body will rotate realistically under gravity when connected by a non-center anchor point.

Joint Target

The target-following behavior of a touch joint is set by passing x and y coordinates to the touchJoint:setTarget() function:

  • touchJoint:setTarget() — Sets the current target (follow) point of the touch joint as represented by targetX and targetY in content space coordinates. This can be any specific content point, the location of the user's touch, the coordinates of some other object to follow, successive points along a path, etc.
touchJoint:setTarget( targetX, targetY )

Damping/Frequency

  • touchJoint.dampingRatio — This number value can range from 0 (no damping) to 1 (critical damping). With critical damping, all oscillations should vanish.

  • touchJoint.frequency — This number value specifies the mass-spring damping frequency in Hz. A low value will result in very low force for target following.

  • touchJoint.maxForce — This number value specifies the maximum allowed force for the touch joint. By default, this attribute is 1000 × the mass of the body, allowing for fairly rapid target following.

Other

Rope Joint

A rope joint connects two objects by a theoretical non-elastic rope. This restricts the maximum distance between the two bodies even if there are other significant forces upon them. The initial arguments are bodies A and B to join, followed by optional localized offset points which can be used to set non-center anchor points for each end of the rope.

local ropeJoint = physics.newJoint( "rope", bodyA, bodyB, offsetA_x, offsetA_y, offsetB_x, offsetB_y )

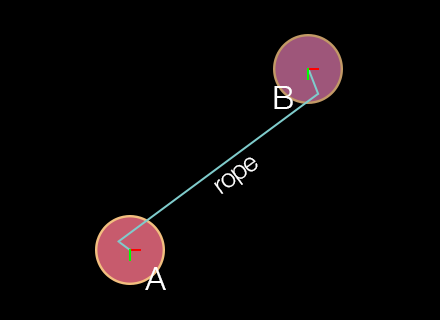
Offset Ends

When configuring a rope joint, the offset values are optional and default to 0 unless set otherwise. Unlike other joints, these x and y values should not be specified in content space. Instead, they should be considered as localized offset values related to either body. For example, if you specify ( ..., 0, 0, 0, 0 ), the rope ends will be attached to the center of each body. However, if you specify ( ..., -20, -20, 10, 10 ), the rope end attached to body A will be offset 20 pixels left and upward of its center point, while the rope end attached to body B will be offset 10 pixels right and downward of its center point.

Maximum Length

The maximum length of the rope can be set via the ropeJoint.maxLength property. Unlike a distance joint which can be used to keep two bodies at a fixed distance apart, the theoretical rope can bend/flex like an actual rope, but the maximum distance will always be constrained to this value.

Other

  • ropeJoint.limitState — Read-only string value that indicates the current limit state of the rope joint: "inactive", "lower", "upper", or "equal".

Gear Joint

To simulate sophisticated mechanical contraptions involving gears, consider using gear joints. This joint can link two bodies — or multiple bodies in sequence — in a gear-like setup. Then, one motor-driven body can realistically power the other bodies just like a real machine.

local gearJoint = physics.newJoint( "gear", bodyA, bodyB, joint1, joint2, ratio )

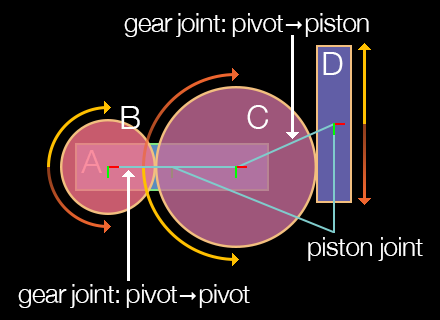
Setup Requirements

The most important distinction of the gear joint is that it operates directly upon two other joints. These two joints must be created before instantiating the gear joint, and they must be either pivot or piston joints. Once declared, one of pivot/piston joints can be powered by its motor and impact the other pivot/piston joint attached to the parent gear joint. The same principle applies to successive joints in a more complex chain configuration, assuming they are properly chained together by other gear joints.

Always destroy gear joints before destroying the associated pivot/piston joints or their bodies. Otherwise, Box2D is liable to crash due to the orphaned gear joint pointers.

Gear Ratio

Another important aspect of the gear joint is the ratio property. This indicates the ratio at which the motor-driven joint drives the corresponding joint in the gear configuration. The value can be either positive or negative, depending on the direction required to create an accurate simulation.

  • gearJoint.ratio — This number specifies the gear ratio, either positive or negative. It can be either set or read. Note that setting the correct ratio can be challenging when setting up a pivot-joined object which drives a piston-joined object, as shown in the diagram. In this case, the gear joint ratio between wheel B and wheel C are 1.0 since wheel B directly drives C. However, you must calculate the ratio for the gear joint which links wheel C to the vertical bar (D), and because wheel C has a larger circumference than wheel B, this ratio would not be 1.0.

Other